单因素方差分析 One Way ANOVA
如果单因素方差分析显示差异具有统计学意义(P<0.05),表示不是所有组的总体均数均相等(至少有一组均数不同于另一组)。如果P>0.05,则表示各组间均数差异无统计学意义。
2种适用的研究设计
1)判断3个及以上独立的组间均数是否存在差异;
2)判断前后变化的差值是否存在差异。
6个假设
假设1:因变量为连续变量;
假设2:有一个包含2个及以上分类、且组别间相互独立的自变量;
假设3:每组间和组内的观测值相互独立;
假设4:每组内没有明显异常值;
假设5:每组内因变量符合正态分布;
假设6:进行方差齐性检验,观察每组的方差是否相等。
整体流程
假设验证
假设4:每组内没有明显异常值
-
Boxplots
如果存在多个异常值,应先把最极端的异常值去掉后,重新检查异常值情况。
异常值的处理方法:
(1) 保留异常值:
1)采用非参数Kruskal-Wallis H检验;
2)用非最极端的值来代替极端异常值(如用第二大的值代替);
3)因变量转换成其他形式;
4)将异常值纳入分析,并坚信其对结果不会产生实质影响。
(2) 剔除异常值:
直接删除异常值很简单,但却是没有办法的办法。当我们需要删掉异常值时,应报告异常值大小及其对结果的影响,最好分别报告删除异常值前后的结果。而且,应该考虑有异常值的个体是否符合研究的纳入标准。如果其不属于合格的研究对象,应将其剔除,否则会影响结果的推论。
假设5:每组内因变量符合正态分布
Shapiro-Wilk正态性检验、偏度和峰度值、直方图等
如果样本量较小(<50),并且对正态Q-Q图或其他图形方法的结果诠释不够有把握,推荐采用Shapiro-Wilk检验。每组自变量都会有一个Shapiro-Wilk正态性检验结果;如果样本量大于50,推荐使用正态Q-Q图等图形方法进行正态判断,因为当样本量较大时,Shapiro-Wilk检验会把稍稍偏离正态分布的数据也标记为有统计学差异,即数据不服从正态分布。
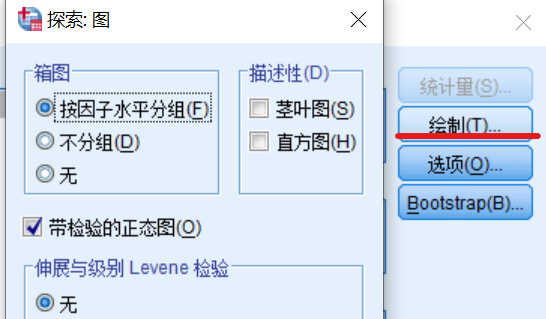
boxplot选择“带检验的正态图”
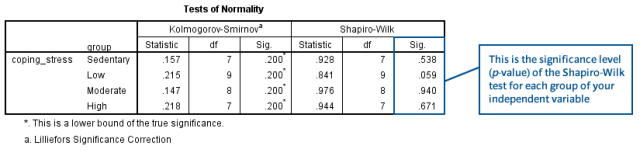
如果数据符合正态分布,显著性水平(蓝框中的Sig.)应该大于0.05。Shapiro-Wilk检验的无效假设是数据服从正态分布,备择假设是数据不服从正态分布。因此,如果拒绝无效假设(P<0.05),表示数据不服从正态分布;如果不能拒绝无效假设,则不能认为数据不服从正态分布。
不服从正态分布的处理方法
(1) 数据转换:对转换后呈正态分布的数据进行单因素方差分析。当各组因变量的分布形状相同时,正态转换才有可能成功。对于一些常见的分布,有特定的转换形式,但是对于转换后数据的结果解释可能比较复杂。
(2) 使用非参数检验:可以使用Kruskal-Wallis H检验等非参数检验方法,但是要注意Kruskal-Wallis H检验和单因素方差分析的无效假设和备择假设不太一致。
(3) 直接进行分析:由于单因素方差分析对于偏离正态分布比较稳健,尤其是在各组样本量相等或近似相等的情况下,而且非正态分布实质上并不影响犯I型错误的概率。因此可以直接进行检验,但是结果中仍需报告对正态分布的偏离。
(4) 检验结果的比较:将转换后和未转换的原始数据分别进行单因素方差分析,如果二者结论相同,则再对未转换的原始数据进行分析。
假设6:进行方差齐性检验,观察每组的方差是否相等
SPSS操作
单因素方差分析(ONEWAY procedure)→事后两两比较(post hoc test)
(1) 点击Analyze > Compare Means > One-Way ANOVA:
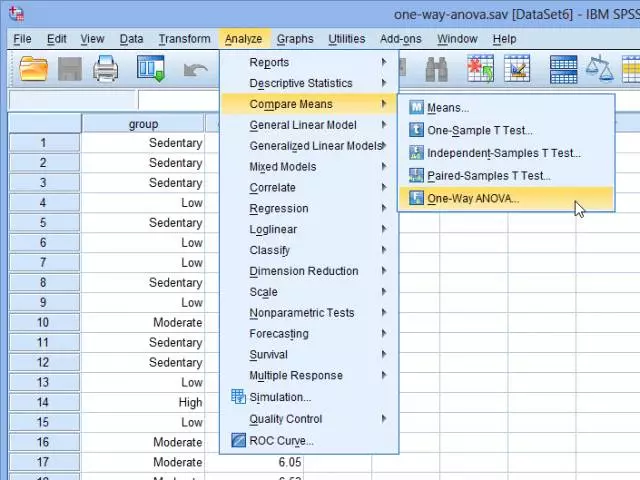
出现One-Way ANOVA对话框:
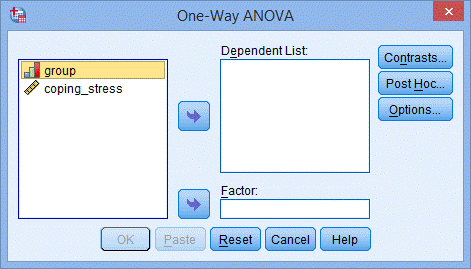
(2) 把因变量coping_stress送入Dependent List框中,自变量group送入Factor框中:
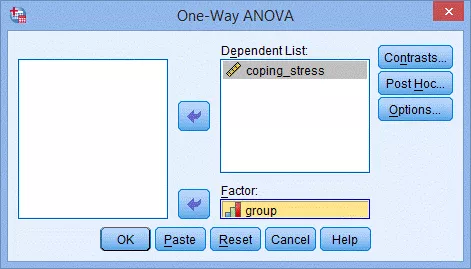
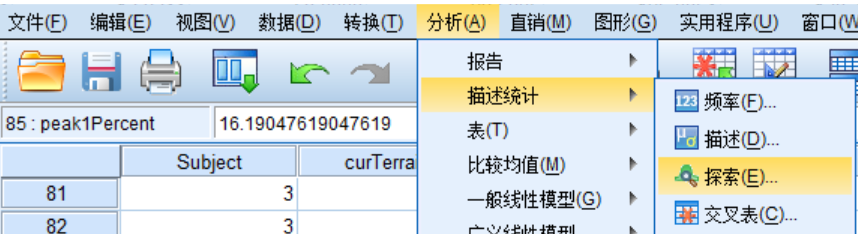
(3) 点击Options,出现One-Way ANOVA: Options对话框:
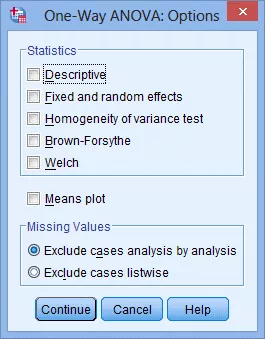
(4) 在Statistics模块勾选Descriptive,Homogeneity of variance test和Welch,同时勾选Means plot:
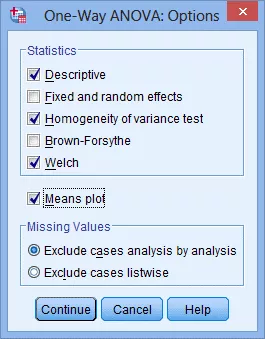
(5) 点击Continue,返回One-Way ANOVA对话框。
(6) 点击Post Hoc,出现One-Way ANOVA: Post Hoc Multiple Comparisons对话框:
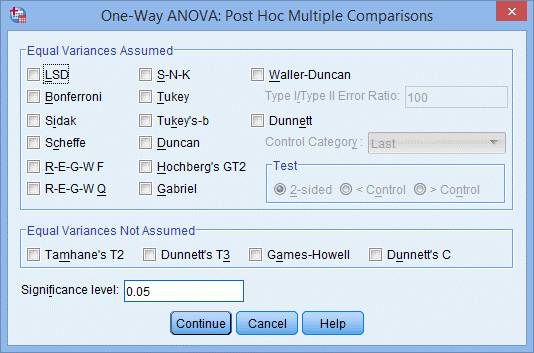
对话框根据方差齐性检验的假设是否满足,分为2个主要区域:
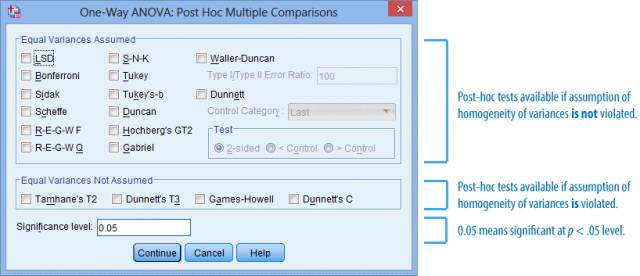
(7) 在Equal Variances Assumed模块内勾选Tukey,在Equal Variances Not Assumed模块内勾选Games-Howell:
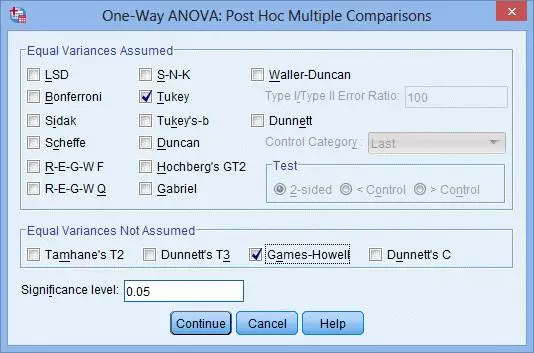
(注) 在Equal Variances Assumed模块内SPSS提供了许多两两比较的方法。例如,LSD法为“最小显著差数法”,是在无校正的前提下,在不同组间进行多次两个独立样本t检验;Bonferroni法是比较流行的方法,同LSD法类似在多组间进行两个独立样本t检验,但是采用了Bonferroni法进行校正。
(8) 可以在Significance level框中修改显著性水平的大小(系统默认为0.05,表示当P<0.05时差异具有统计学意义,可以将其数值修改为0.01)。
(9) 点击Continue,返回One-Way ANOVA对话框。
(10) 点击OK,输出结果。
一般线性模型(GLM procedure)求效应量(偏η2)
(1) 点击Analyze > General Linear Model > Univariate…:
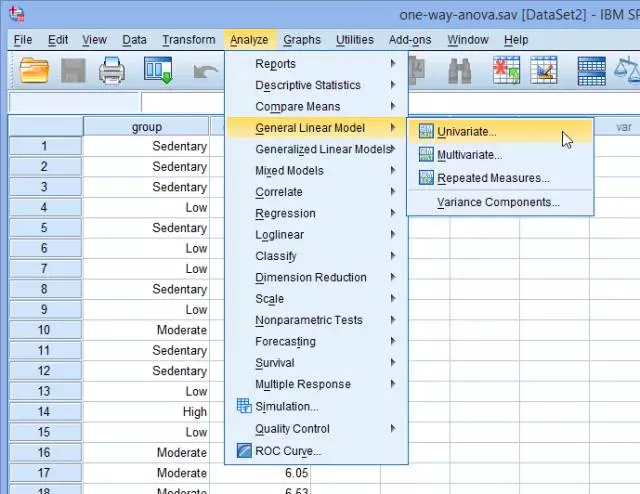
出现Univariate对话框:
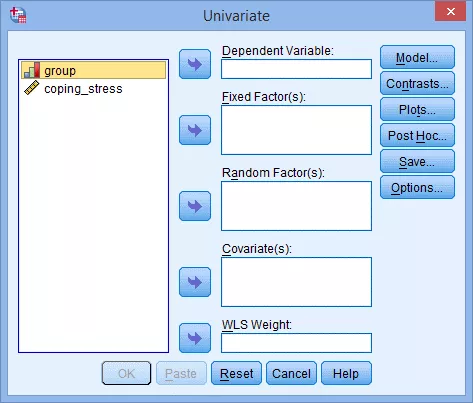
(2) 把因变量coping_stress送入Dependent List框中,自变量group送入Fixed Factor(s)框中:
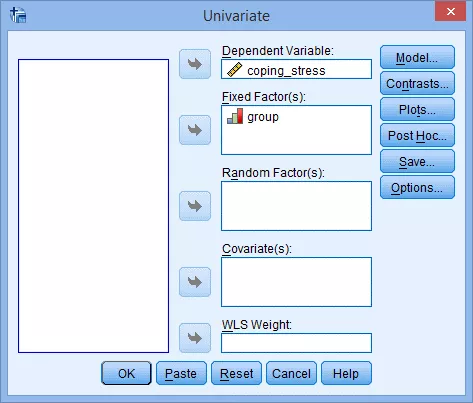
(3) 点击Options…,出现 Univariate: Options对话框:
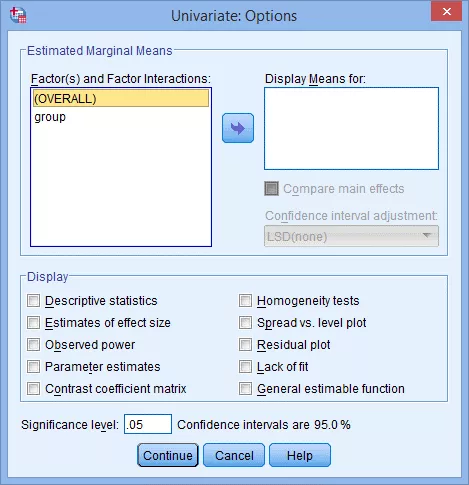
(4) 在Display模块内勾选Estimates of effect size:
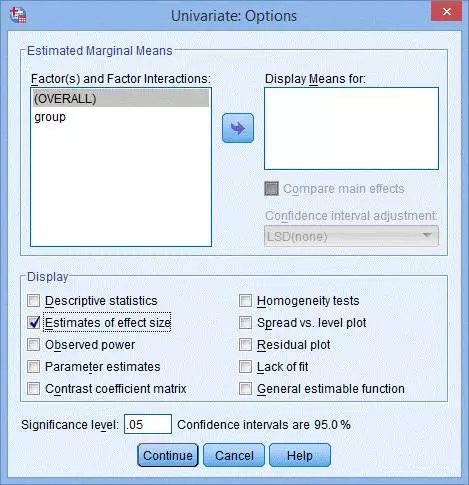
(5) 点击Continue,返回Univariate对话框。
(6) 点击OK,输出结果。
一般线性模型(GLM procedure)→自定义组间比较(custom contrasts)
如果只关心特定组别间的差异,你需要知道如何进行自定义比较(custom contrasts),以及如何对多重比较结果进行调整,这就要用到SPSS软件中的Syntax Editor窗口编写相应程序语句。当满足方差齐性条件时,推荐采用GLM程序进行自定义组间比较。
前2步操作同“2. 一般线性模型(GLM procedure)求效应量(偏η2)”的前2步操作,这里不再赘述。接下来:
(1) 点击Paste,出现IBM SPSS Statistics Syntax Editor窗口:
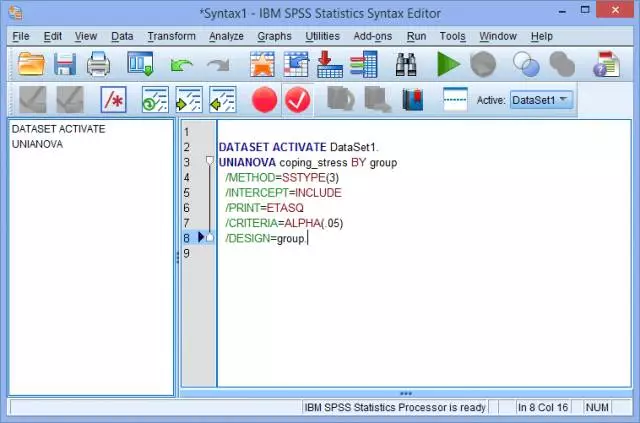
(2) 在 /PRINT 和 /CRITERIA两行中间,输入 /LMATRIX = group -1 1 0 0:
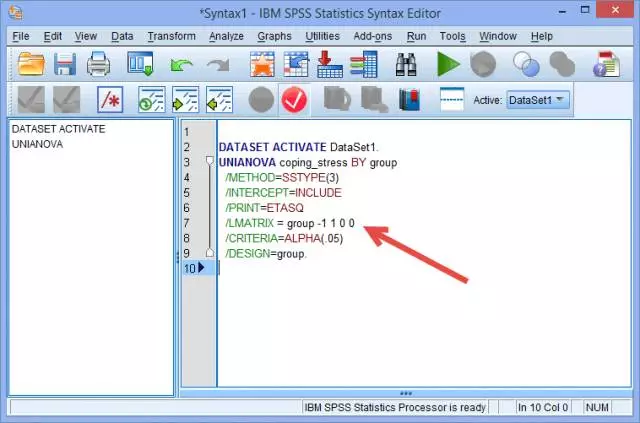
/LMATRIX= 旨在告诉SPSS我们要做一个自定义假设;group表示将要进行比较的自变量组别;-1 1 0 0表示要进行比较的系数,系数的顺序和SPSS里输入的组别顺序有关:这里从左到右(-1 1 0 0)分别对应着久坐组、“低”、“中”和“高”体力活动组,表示将“低”体力活动组与久坐组进行比较。
**(注)**自定义比较包括了简单比较(simple contrasts)和复合比较(complex contrasts)。简单比较为只比较自变量某两个组别间的差异,需要建立线性比较函数(linear contrast,φ)。它包含一系列系数和每个组别对应的均数,系数取值只能为1,-1,0。我们把要比较的两组的系数分别赋值为1和-1,其他不比较的组别系数赋值为0。
本例中久坐组系数为-1,“低”体力活动组系数为1,其他组别均为0,则是要比较久坐组和“低”体力活动组的CWWS得分差异,看二者的平均CWWS得分差值是否为0(用“低”体力活动组得分减去久坐组得分,即系数为1的组别减去系数为-1的组别,以系数为-1的组别为参照组,系数赋值的正负与研究设计和研究假设有关)。
(3) 用/LMATRIX指令增加另外2种比较:
/LMATRIX = group -1 1/3 1/3 1/3
/LMATRIX = group -1/2 -1/2 1/2 1/2
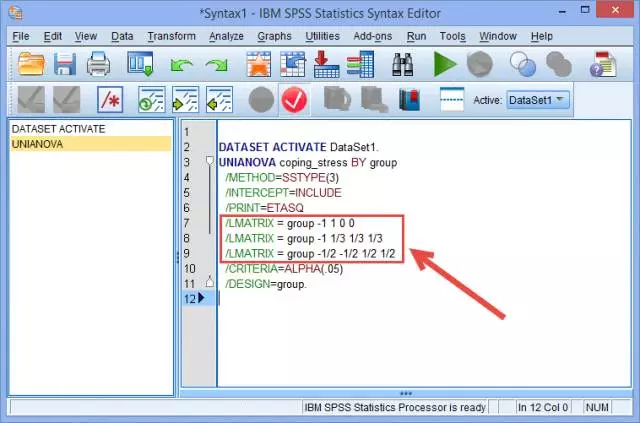
**(注)**复合比较为比较自变量超过2个组别的组合间的差异,如比较B组与C、D两组的组合间的差异,或C、D两组间的组合与A、D两组间组合的差异。同样采用线性比较函数的方法,某组合的系数赋值为1或-1除以组合内的组数,但是要保证要比较的组间组合与另一组(组合)的所有系数加起来为0,系数赋值的正负与研究设计和研究假设有关。
本例中,/LMATRIX = group -1 1/3 1/3 1/3表示“低”、“中”和“高”体力活动组的组合整体与久坐组CWWS得分差异的比较,/LMATRIX = group -1/2 -1/2 1/2 1/2表示“中”和“高”体力活动组的组合与“低”体力活动组和久坐组组合的比较。
(4) 多重比较的校正
接下来,我们需要校正显著性水平(α),通常也可以校正每次比较的P值和可信区间,得到调整后P值和联合可信区间(simultaneous confidence intervals)。我们首先采用Bonferroni方法对显著性水平α进行校正,公式如下:
调整后α=调整前α ÷ 比较的次数
本例中我们需要进行3次比较,则调整后α=0.05÷3=0.01667。
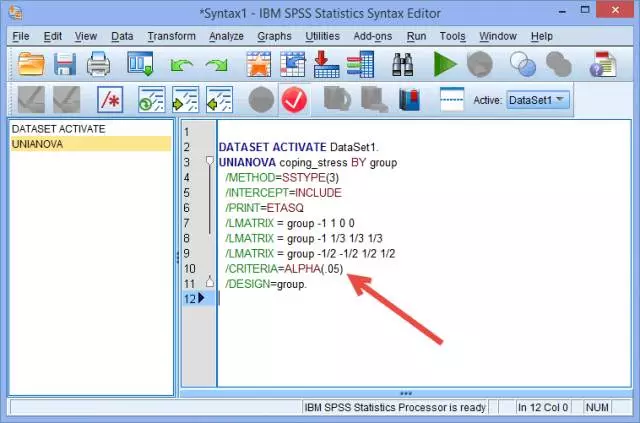
(5) 箭头标注处为SPSS软件默认的显著性水平α=0.05:
/CRITERIA=ALPHA(.05)
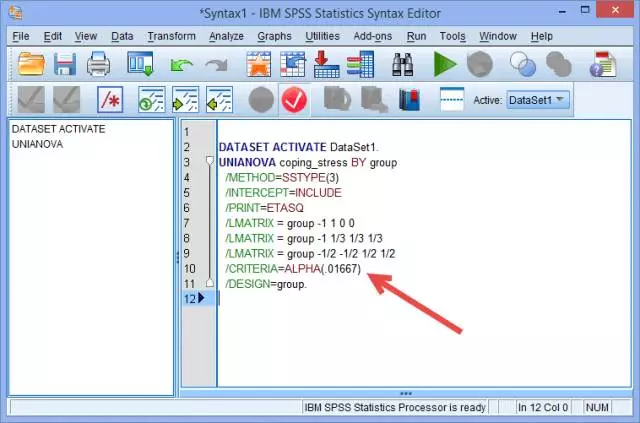
(6) 我们将其改为调整后的显著性水平α=0.1667:
/CRITERIA=ALPHA(.01667)
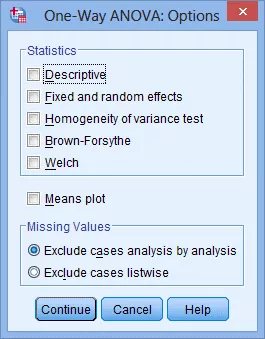
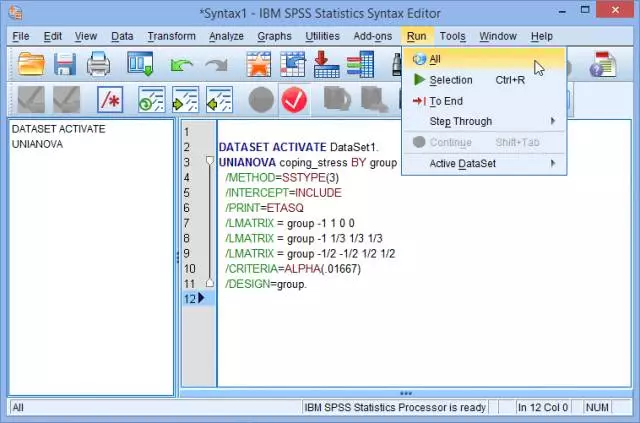
(7) 在菜单栏点击Run > All:
单因素方差分析(ONEWAY procedure)→自定义组间比较(custom contrasts)
虽然ONEWAY程序有很多缺点,但却是不满足方差齐性条件时唯一可用的方法。前2步操作同“1. 单因素方差分析(ONEWAY procedure)→两两比较(post hoc test)”的前2步操作,这里不再赘述。接下来:
(1) 点击Contrasts,出现 One-Way ANOVA: Contrasts对话框:
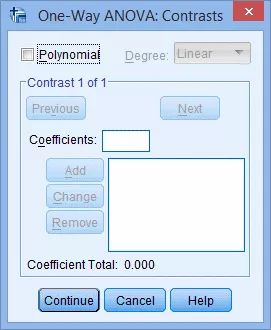
(2) 在Coefficients模块中输入第一组比较(如-1 1 0 0)的第一个系数,点击Add:
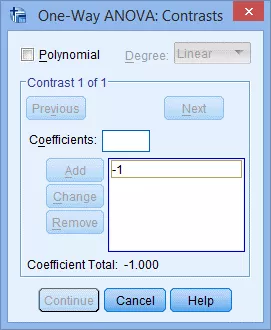
(3) 在Coefficients模块中输入第一组比较(如-1 1 0 0)的其他系数,点击Add:
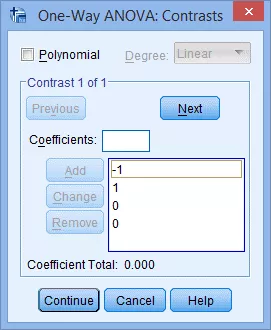
(4) 点击Next,输入新的自定义比较组,此时下图中红框区域内将变为 –Contrast 2 of 2–:

(5) 按照之前的方式输入第二个比较组(如-1 1/3 1/3 1/3):
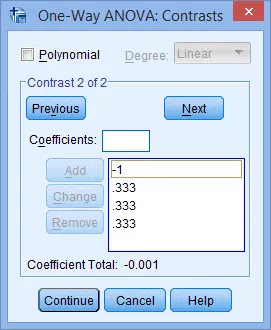
**注:**Coefficients模块中无法输入分数,最多只能输入3位小数的数值来代替。因此本例中输入0.333代替1/3,但是由于最后总和不等于1(0.333×3=0.999),因此我们将在后面的第(9)(10)步中进行调整。
(6) 继续点击Next,输入新的自定义比较组,此时下图中红框区域内将变为 –Contrast 3 of 3–:
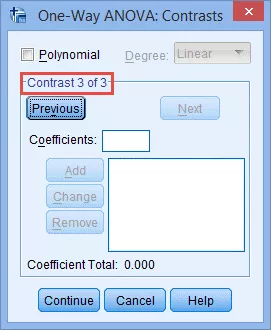
(7) 按照之前的方式输入第三个比较组(如-1/2 -1/2 1/2 1/2):
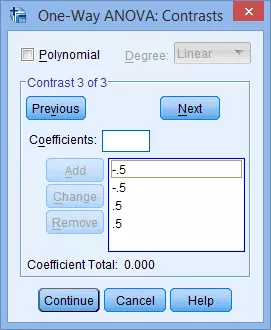
(8) 点击Continue,返回One-Way ANOVA对话框。
(9) 点击Paste,进入IBM SPSS Statistics Syntax Editor窗口:
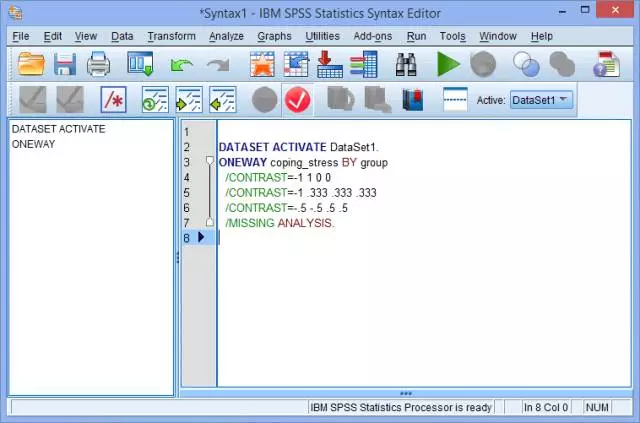
(10) 手动增加小数位数,如把小数位数从3位改为10位(0.333改为0.3333333333):
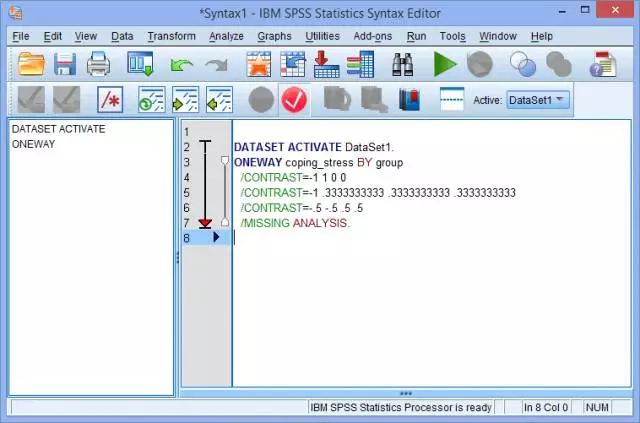
(11) 在菜单栏中点击Run > All: