Intention Recgonition for Exoskeleton
intention定义: walk/stand
assistance exoskeleton system
-
支持4种state: L swing, R swing, Double stance(L), Double stance(R)
-
control
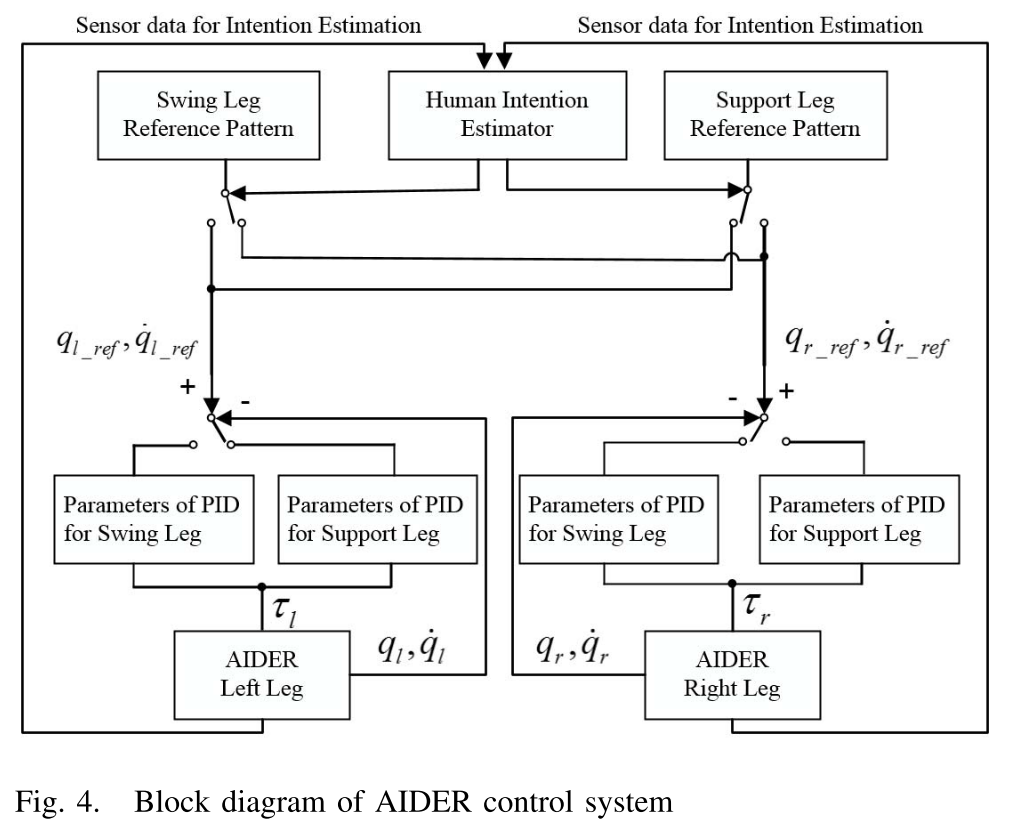
Methods
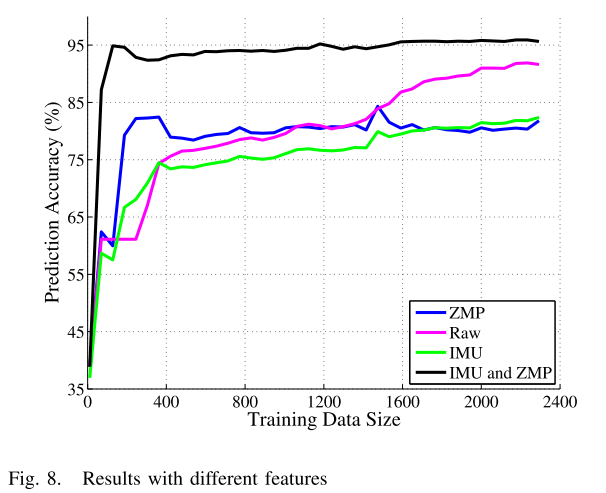
online SVM; features: ZMP(Zero Moment Point), IMU
-
ZMP
-
concept: The distributed floor reaction force can be replaced by a single force R acts on ZMP.
-
ZMP can be obtained from ground reaction force (GRF) measurement or inverse dynamics of system.
-
calculation
$r=[\delta\ \varepsilon\ 0]$ is a vector on the ground and $ \rho(\delta, \varepsilon) $ is the vertical force acted on unit area at point $ r$. So the sum of vertical force is like $f_{z}=\int_{s} \rho(\delta, \varepsilon) d S$
torque at $p=\left[p_{x}\ p_{y}\ 0\right]$ is $\tau_{n}(p) $.
$\begin{aligned} \tau_{nx} &=\int_{S}(\delta-p_{x}) \rho(\delta, \varepsilon) d S \\ \tau_{ny} &=\int_{S}(\varepsilon-p_{y}) \rho(\delta, \varepsilon) d S \\ \tau_{nz} &=0 \end{aligned}$
At ZMP $\tau_{n x}=0, \tau_{n y}=0$ , we can get
$\begin{aligned} p_{x} &=\frac{\int_{S} \delta \rho(\delta, \varepsilon)}{\int_{S} \rho(\delta, \varepsilon)}\\p_{y} &=\frac{\int_{S} \varepsilon \rho(\delta, \varepsilon)}{\int_{S}\rho(\delta, \varepsilon)}\end{aligned}$
-
As $\rho(\delta, \varepsilon) $ is the distribution of reaction force on foot, ZMP p is also the center of pressure(COP).
-
| ZMP for one foot | ZMP of system |
|---|---|
| $P_{l x} =\frac{\sum_{i=1}^{7} p_{i}^{x} f_{i}}{\sum_{i=1}^{7} f_{i}}$ $ P_{l y} =\frac{\sum_{i=1}^{7} p_{i}^{y} f_{i}}{\sum_{i=1}^{7} f_{i}}$ $F_{l} =\sum_{i=1}^{7} f_{i}$ |
$Z M P_{x} =\frac{P_{l x} F_{l}+P_{r x} F_{r}}{F_{l}+F_{R}}$ $Z M P_{y} =\frac{P_{l y} F_{l}+P_{r y} F_{r}}{F_{l}+F_{R}}$ |
-
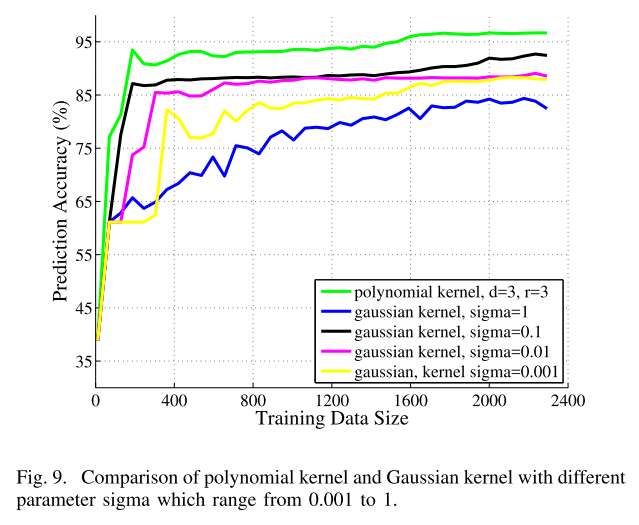
SVM
polynomial kernel; Gaussian kernel
Thoughts/Comments
- TODO ZMP之后应该用得上,这个推导可以看一眼